مدل تعدیل به بررسی این سوال میپردازد که آیا پیش بینی یک متغیر وابسته (Y)، از روی یک متغیر مستقل (X)، در سطوح مختلف یک متغیر سوم (مثلا Z) متفاوت است؟
بارون و کنی (۱۹۸۶) متغیر تعدیل کننده را اینگونه تعریف نمودهاند: ” یک متغیر کیفی (به عنوان مثال، جنس، نژاد، طبقه) یا یک متغیر کمی (مانند سطح پاداش) است که جهت و یا شدت رابطه بین یک متغیر پیشبین و یک متغیر ملاک را تحت تأثیر قرار می دهد” (صفحهی ۱۱۷۴): افزایش، کاهش و یا تغییر تاثیر پیش بینی کننده.
میخواهیم ببینیم آیا جنسیت میتواند بر رابطهی بین حمایت اجتماعی (X) و افسردگی (Y) تأثیر بگذارد. در اینجا جنسیت به عنوان متغیر تعدیل کننده (Z) معرفی میشود. سئوالی که در اینجا مطرح میشود این است که آیا رابطه بین حمایت اجتماعی (X) و افسردگی (Y) در ن و مردان متفاوت است؟
به طور خاص در قالب تجزیه و تحلیل همبستگی، متغیر تعدیل کننده یک متغیر سوم است که همبستگی مرتبه صفر بین دو متغیر دیگر را تحت تاثیر قرار می دهد.
اثر تعدیل کننده را در چارچوب تجزیه و تحلیل واریانس (ANOVA) نیز میتوان تعریف کرد. اثرات تعدیل معمولا تحت عنوان تعامل بین عوامل یا متغیرها مورد بحث قرار میگیرد، که در آن اثر یک متغیر به سطوح متغیر دیگر موجود در تجزیه و تحلیل بستگی دارد. به بیان دیگر، تعدیل به بررسی تعامل آماری بین دو متغیر مستقل در پیش بینی یک متغیر وابسته گفته میشود (شکل ۱).
شکل ۱: نمودار مسیر برای مدل تعدیل
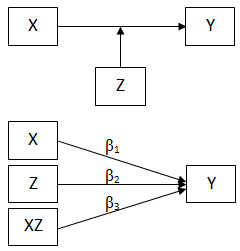
اثرات تعدیل را با استفاده از رگرسیون چندگانه نیز میتوان آزمون کرد که در آن برای آزمون فرضیه تعدیل ارائه شده یک رگرسیون چندگانه با سه عبارت پیشبین انجام میدهیم: (۱) X، (۲) Z و (۳) عبارت تعامل یعنی XZ (شکل ۱).
معادلهی رگرسیون نیز به صورت زیر خواهد بود:
![]()
β۱: ضریب مسیر بین X و Y وقتی ۰=Z
β۲: ضریب مسیر بین Z و Y وقتی ۰=X
i1: عرض از مبدأ معادله
e1: باقیمانده معادله
ضریب رگرسیون مربوط به عبارت تعامل (β۳) برآوردی از اثر تعدیل فراهم میکند. چنانچه β۳ تفاوت معنیداری با صفر داشته باشد، تعدیل رابطه Y – X در داده ها معنادار است. ترسیم اثر تعاملی به تفسیر تعدیل کمک میکند. این نمودار نشان میدهد که چگونه متغیر تعدیل کننده شیب خط رگرسیون برای پیشبینی Y براساس مقادیر X را تحت تاثیر قرار میدهد.
منبع: Jose, Paul E. (2013). Doing Statistical Mediation and Moderation. Guilford Press
درباره این سایت